Predicting Future Blood Donations in R
November 16, 2017
In addition to refreshing data analysis skills, our goal is to build a statistical model to predict if a blood donor will donate within a given time window, which is March 2007.
The Rmarkdown document can be found at the project repository.
Table of Contents
- Data
- Exploratory Data Analysis
- Logistic Regression Analysis
- Goodness of Fit
- Predictions
- Future Updates
Data
The provided datasets, trainingData.csv and testData.csv contain the following variables:
X1: ID of donor.Months since Last Donation: Number of months since the donor’s most recent blood donation.Number of Donations: Total number of donations the donor has made.Total Volume Donated: Total amount of blood the donor has donated in cubic centimeters.Months since First Donation: Number of months since the donor’s first blood donation.Made Donation in March 2007: The explanatory variable or result -1if they donated blood,0if they did not donate blood in March 2007.
We can view the first couple of observations of the datasets below:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
# Set working directory and load packages
getwd()
## [1] "/home/lila/Documents/Projects/blood-donations"
library(tidyverse)
library(gridExtra)
library(aod)
library(corrplot)
# Import datasets; adjust if datasets are in a different directory
testData = read.csv("data/testData.csv", header = TRUE)
trainingData = read.csv("data/trainingData.csv", header = TRUE)
# Display first rows of datasets
head(trainingData)
## X Months.since.Last.Donation Number.of.Donations
## 1 619 2 50
## 2 664 0 13
## 3 441 1 16
## 4 160 2 20
## 5 358 1 24
## 6 335 4 4
## Total.Volume.Donated..c.c.. Months.since.First.Donation
## 1 12500 98
## 2 3250 28
## 3 4000 35
## 4 5000 45
## 5 6000 77
## 6 1000 4
## Made.Donation.in.March.2007
## 1 1
## 2 1
## 3 1
## 4 1
## 5 0
## 6 0
head(testData)
## X Months.since.Last.Donation Number.of.Donations
## 1 659 2 12
## 2 276 21 7
## 3 263 4 1
## 4 303 11 11
## 5 83 4 12
## 6 500 3 21
## Total.Volume.Donated..c.c.. Months.since.First.Donation
## 1 3000 52
## 2 1750 38
## 3 250 4
## 4 2750 38
## 5 3000 34
## 6 5250 42
Since testData is our testing data set, it does not have Made Donation in March 2007 variable.
Renaming Variables
To make the data analysis more simple, we will rename the variables using colnames():
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# Rename variables in testData and trainingData
colnames(testData) <- c("ID", "mosLastDo", "numDonations", "totVol", "mosFirstDo")
colnames(trainingData) <- c("ID", "mosLastDo", "numDonations", "totVol", "mosFirstDo", "madeDonation")
# Display first rows of datasets (to confirm name changes)
head(trainingData)
## ID mosLastDo numDonations totVol mosFirstDo madeDonation
## 1 619 2 50 12500 98 1
## 2 664 0 13 3250 28 1
## 3 441 1 16 4000 35 1
## 4 160 2 20 5000 45 1
## 5 358 1 24 6000 77 0
## 6 335 4 4 1000 4 0
head(testData)
## ID mosLastDo numDonations totVol mosFirstDo
## 1 659 2 12 3000 52
## 2 276 21 7 1750 38
## 3 263 4 1 250 4
## 4 303 11 11 2750 38
## 5 83 4 12 3000 34
## 6 500 3 21 5250 42
Since the explanatory variable madeDonation results in two outcomes (either the donor donates in March 2007 or not), we consider building a logistic regression model for our data. However, before we proceed to building the model, we’ll perform some EDA (Exploratory Data Analysis) to find more about our data.
Exploratory Data Analysis
First, we need to make the binary factor madeDonation is read as a categorical variable. Otherwise, the 0 and 1 values will be read as continuous variables instead of two groups.
1
2
3
4
5
6
7
# Turn madeDonation into factors instead of continuous
trainingData$madeDonation <- factor(trainingData$madeDonation)
contrasts(trainingData$madeDonation)
## 1
## 0 0
## 1 1
trainingData$ID <- factor(trainingData$ID)
Summary of trainingData:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
summary(trainingData)
## ID mosLastDo numDonations totVol
## Min. : 0.0 Min. : 0.000 Min. : 1.000 Min. : 250
## 1st Qu.:183.8 1st Qu.: 2.000 1st Qu.: 2.000 1st Qu.: 500
## Median :375.5 Median : 7.000 Median : 4.000 Median : 1000
## Mean :374.0 Mean : 9.439 Mean : 5.427 Mean : 1357
## 3rd Qu.:562.5 3rd Qu.:14.000 3rd Qu.: 7.000 3rd Qu.: 1750
## Max. :747.0 Max. :74.000 Max. :50.000 Max. :12500
## mosFirstDo madeDonation
## Min. : 2.00 0:438
## 1st Qu.:16.00 1:138
## Median :28.00
## Mean :34.05
## 3rd Qu.:49.25
## Max. :98.00
Boxplots
We plot Boxplots of the two groups to see if there are any patterns:
1
2
3
4
5
6
# Boxplots
plot01 <- ggplot(data = trainingData) + geom_boxplot(aes(x = madeDonation, y = numDonations)) + labs(title = "Number of Donations", subtitle = "Made Donations vs. No Donations")
plot02 <- ggplot(data = trainingData) + geom_boxplot(aes(x = madeDonation, y = totVol)) + labs(title = "Total Volume Donated", subtitle = "Made Donations vs. No Donations")
plot03 <- ggplot(data = trainingData) + geom_boxplot(aes(x = madeDonation, y = mosLastDo)) + labs(title = "Months since Last Donation", subtitle = "Made Donations vs. No Donations")
plot04 <- ggplot(data = trainingData) + geom_boxplot(aes(x = madeDonation, y = mosFirstDo)) + labs(title = "Months since First Donation", subtitle = "Made Donations vs. No Donations")
grid.arrange(plot01, plot02, plot03, plot04, ncol = 2)
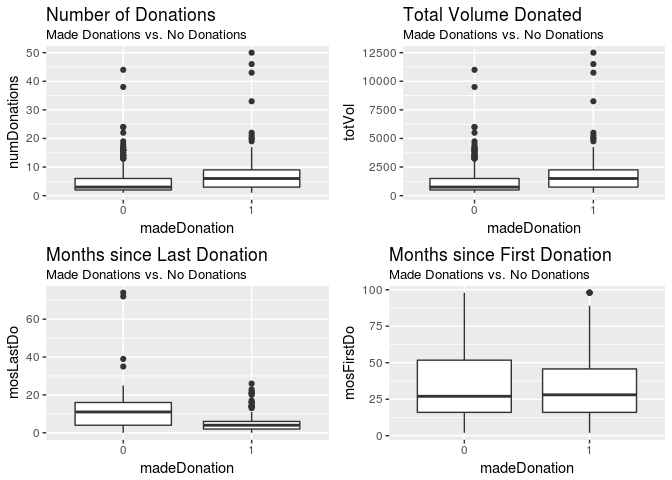
numDonations and totVol look similar, which makes sense - the total amount of blood donated should increase as the number of donations increase. We can see this by looking at their correlation:
1
2
3
4
5
6
7
8
TDselect <- select(trainingData, mosLastDo, numDonations, totVol, mosFirstDo)
cor1 <- round(cor(TDselect), 2)
cor1
## mosLastDo numDonations totVol mosFirstDo
## mosLastDo 1.00 -0.16 -0.16 0.19
## numDonations -0.16 1.00 1.00 0.62
## totVol -0.16 1.00 1.00 0.62
## mosFirstDo 0.19 0.62 0.62 1.00
Both numDonations and totVol have a correlation of 1.00. Hence, we can leave out totVol in the model.
Feature Engineering
If we create a new variable that takes the average of each donation (totVol / numDonations), each observation will be the same (250 cubic centimeters). However, the number of donations varies among the donors, so we will create a variable involving mosFirstDo and mosLastDo. We get donFreq, which is the length of time between a donor’s first and last donation divided by the total number of donations.
Some donors have the same values for mosFirstDo and mosLastDo, indicating that they are first-time donors. We can create a new binary variable firstTime to indicate first-time donors and see if there is a significant effect.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
TD2 <- mutate(trainingData, donFreq = (mosFirstDo - mosLastDo) / numDonations)
TD2 <- mutate(TD2, firstTime = ifelse(mosFirstDo == mosLastDo, "0", "1"))
TD2$firstTime <- factor(TD2$firstTime) # turn into factors
head(TD2)
## ID mosLastDo numDonations totVol mosFirstDo madeDonation donFreq
## 1 619 2 50 12500 98 1 1.920000
## 2 664 0 13 3250 28 1 2.153846
## 3 441 1 16 4000 35 1 2.125000
## 4 160 2 20 5000 45 1 2.150000
## 5 358 1 24 6000 77 0 3.166667
## 6 335 4 4 1000 4 0 0.000000
## firstTime
## 1 1
## 2 1
## 3 1
## 4 1
## 5 1
## 6 0
Logistic Regression Analysis
We will consider a simple logistic linear model for our data.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
model01 <- glm(madeDonation ~ mosLastDo + numDonations + mosFirstDo + donFreq + firstTime, family = binomial(link = 'logit'), data = TD2)
summary(model01)
##
## Call:
## glm(formula = madeDonation ~ mosLastDo + numDonations + mosFirstDo +
## donFreq + firstTime, family = binomial(link = "logit"), data = TD2)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.9825 -0.7195 -0.4795 -0.1432 2.6478
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -1.07482 0.29128 -3.690 0.000224 ***
## mosLastDo -0.09708 0.02121 -4.576 4.74e-06 ***
## numDonations 0.06880 0.03982 1.728 0.084052 .
## mosFirstDo -0.01027 0.01159 -0.886 0.375721
## donFreq -0.10569 0.06382 -1.656 0.097723 .
## firstTime1 1.29274 0.38118 3.391 0.000695 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 634.29 on 575 degrees of freedom
## Residual deviance: 544.29 on 570 degrees of freedom
## AIC: 556.29
##
## Number of Fisher Scoring iterations: 5
At the significance level of alpha = 0.05, mosLastDo and firstTime are statistically significant.
- For every unit change in
mosLastDo, the log odds of donating in March 2007 reduces by0.09708. - If the donor is NOT a first-time donor (
firstTime1), the log odds of donating in March 2007 changes by1.29274.
Wald test for firstTime
We will perform a Wald test the overall effectiveness of firstTime.
1
2
3
4
5
6
wald.test(b = coef(model01), Sigma = vcov(model01), Terms = 5)
## Wald test:
## ----------
##
## Chi-squared test:
## X2 = 2.7, df = 1, P(> X2) = 0.098
The chi-squared statistic of 2.7 with 1 degrees of freedom and a p-value of 0.098 indicates that the overall effect of firstTime is statistically insignificant.
Odds Ratios
We can obtain the odds-ratio and 95% CI from the coefficients:
1
2
3
4
5
6
7
8
9
10
exp(cbind(OR = coef(model01), confint(model01)))
## Waiting for profiling to be done...
## OR 2.5 % 97.5 %
## (Intercept) 0.3413601 0.1881293 0.5928383
## mosLastDo 0.9074839 0.8694857 0.9451285
## numDonations 1.0712223 0.9938612 1.1628537
## mosFirstDo 0.9897842 0.9671976 1.0123875
## donFreq 0.8997038 0.7857770 1.0095484
## firstTime1 3.6427465 1.7525382 7.8386961
For a unit increase in mosLastDo, the odds of donating in March 2007 increases by 0.9074839.
Goodness of Fit
Before we can start predicting with our model, we will test the Full and Reduced models with a Likelihood Ratio Test.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
# Create reduced model
model02 <- glm(madeDonation ~ mosLastDo + firstTime, family = binomial(link = 'logit'), data = TD2)
summary(model02)
##
## Call:
## glm(formula = madeDonation ~ mosLastDo + firstTime, family = binomial(link = "logit"),
## data = TD2)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.1192 -0.7487 -0.5422 -0.2438 2.6574
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -0.97103 0.28677 -3.386 0.000709 ***
## mosLastDo -0.11000 0.01822 -6.036 1.58e-09 ***
## firstTime1 0.83258 0.28306 2.941 0.003268 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 634.29 on 575 degrees of freedom
## Residual deviance: 573.01 on 573 degrees of freedom
## AIC: 579.01
##
## Number of Fisher Scoring iterations: 5
# Likelihood Ratio test bt. Full and Reduced
anova(model01, model02, test = "LRT")
## Analysis of Deviance Table
##
## Model 1: madeDonation ~ mosLastDo + numDonations + mosFirstDo + donFreq +
## firstTime
## Model 2: madeDonation ~ mosLastDo + firstTime
## Resid. Df Resid. Dev Df Deviance Pr(>Chi)
## 1 570 544.29
## 2 573 573.01 -3 -28.716 2.569e-06 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
A p-value of 2.569e-06 indicates that the full model is a better fit than the reduced model. Compared to the reduced model, the full model’s AIC is slightly lower (556.29 to 579.01).
Predictions
Before we can start predicting, we need to adjust testData with the same variables as trainingData.
1
2
3
4
5
6
7
8
9
10
11
testData2 <- mutate(testData, donFreq = (mosFirstDo - mosLastDo) / numDonations)
testData2 <- mutate(testData2, firstTime = ifelse(mosFirstDo == mosLastDo, "0", "1"))
testData2$firstTime <- factor(testData2$firstTime)
head(testData2)
## ID mosLastDo numDonations totVol mosFirstDo donFreq firstTime
## 1 659 2 12 3000 52 4.166667 1
## 2 276 21 7 1750 38 2.428571 1
## 3 263 4 1 250 4 0.000000 0
## 4 303 11 11 2750 38 2.454545 1
## 5 83 4 12 3000 34 2.500000 1
## 6 500 3 21 5250 42 1.857143 1
We will create a new data frame newDF to store our predicted probabilities in a new column donateP.
1
2
3
4
5
6
7
8
9
10
11
# Create a base DF to be used in predictions
newDF <- with(testData2, data.frame(ID = ID, mosLastDo = mosLastDo, numDonations = numDonations, mosFirstDo = mosFirstDo, donFreq = donFreq, firstTime = factor(firstTime)))
newDF$donateP <- predict(model01, newdata = newDF, type="response")
head(newDF)
## ID mosLastDo numDonations mosFirstDo donFreq firstTime donateP
## 1 659 2 12 52 4.166667 1 0.4688002
## 2 276 21 7 38 2.428571 1 0.1206789
## 3 263 4 1 4 0.000000 0 0.1922574
## 4 303 11 11 38 2.454545 1 0.3223996
## 5 83 4 12 34 2.500000 1 0.5104633
## 6 500 3 21 42 1.857143 1 0.6778565
Submission
After predictions, we will then use select() from the dplyr package to create another data frame for our submission, which only includes the donor’s ID and the predicted probability. The columns in submissionData are then renamed to the proper names for the submission format.
1
2
3
4
5
6
7
8
9
10
11
12
13
submissionData <- select(newDF, ID, donateP)
colnames(submissionData) = c("X1", "Made Donation in March 2007") # rename columns to submission format
# Save submissionData as CSV format
write.csv(submissionData, file = "submissionData.csv", row.names = FALSE)
head(submissionData)
## X1 Made Donation in March 2007
## 1 659 0.4688002
## 2 276 0.1206789
## 3 263 0.1922574
## 4 303 0.3223996
## 5 83 0.5104633
## 6 500 0.6778565
With our submission file created and exported, we are about done! All that is left is to submit it!
Future Updates
After the first submission, the next step in this project is to see whether we can improve the performance of our model.